Can the Y Values Repeat in a Function

You lot have worked with relations and functions in the past. Let'due south refresh our memories and add together a few more than details. A relation is simply a set of input and output values, represented in ordered pairs. It is a relationship between sets of data. Any gear up of ordered pairs may be used in a relation. No special rules demand employ to a relation. Consider this example of a relation : The human relationship between eye color and student names. (x,y) = (eye colour, student's proper noun) Set A = {(green,Steve), (blue,Elaine), (dark-brown,Kyle), (green,Marsha), (blue,Miranda), (brownish, Dylan)} Discover that the x-values (eye colors) get repeated. The scatter plot and the graph, shown beneath, are also examples of relations. The thing to discover about them is that they likewise allow for one x-value to take more than one corresponding y-value. Points such as ( 1 ,one) and ( 1 ,2) can BOTH vest to the same relation. Relation: {( 1 ,1),( 1 ,2),(3,3),(4,4),( 5 ,v),( 5 ,6),(6,4)} Relation: ; allows for points such as ( ii ,one.414) and ( 2 ,-1.414). If y'all add a "specific rule" to a relation, yous get a office. A function is a fix of ordered pairs in which each 10-element has only I y-chemical element associated with it. While a function may Not have 2 y-values assigned to the same x-value, information technology may accept two x-values assigned to the aforementioned y-value. Not OK for a role: {( 5 ,1),( five ,4)} OK for a office: {(5, ii ),(4, two )} Function: each ten-value has only 1 y-value! Allow'south arrange our previous examples then they fit the function "definition". If we remove duplicate center colors, the middle color example will exist a function: (x,y) = (eye color, student's name) Prepare B = {(blue,Steve), (green,Elaine), (brown,Kyle)} Ready B is a function . And now the graphs: If nosotros remove (1,2) and (5,half dozen), we will accept a office. Function: {( i ,1), (iii,3),(iv,four),( 5 ,v), (6,4)} If nosotros change the ± sign to just a + sign, we volition take a function. Function: Observe that vertical lines on the graphs arrive articulate if an x-value had more than 1 y-value. If the vertical lines intersected the graph in more than ane location, we had a relation, NOT a function. Vertical line test for functions : Any vertical line intersects the graph of a role in but Ane point. 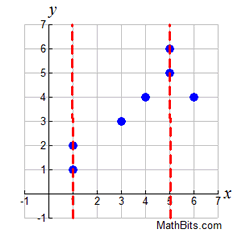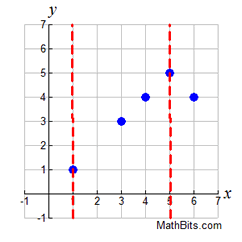Given that relation A = {(iv,3), (k,5), (7,-iii), (three,2)}. Which of the following values for k will brand relation A a function?a) three b) four c) six Solution: Choice c. The 10-values of iii and 4 are already used in relation A. If they are used once again (with a different y-value), relation A will not be a function. Which of the following graphs represents a function? Solution: Choice b. A vertical line drawn on this graph will intersect the graph in but one location, making information technology a part. Vertical lines on the other three graphs will intersect the graph in more than 1 location, or as in part a, will intersect in an infinite number of points (all points). Calculators graph functions! 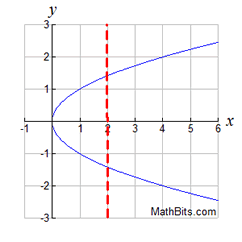When you desire to graph lines, you 1. solve the equation for "y =", produce a chart of points (a T-nautical chart), and plot, or 2. solve the equation for "y =" plot the y-intercept and utilize slope to plot the line, or 3. solve the equation for "y =" and enter the equation in your graphing calculator. By solving for "y =", you are actually identifying a "function". If you can solve an equation for "y =", then the equation is a "part". fourx + 2y = x iiy = -4x + 10 y = -2ten + 5 (a function!) This equation can now be entered into a graphing calculator for plotting. Most calculators (including the TI-84+ serial) tin only handle graphing functions. The equation (office) must be in "y = " form before you tin enter it in the calculator. BUT ... what most y two = 10 ? If we solve for "y =", we get , which nosotros saw, at top of this page, was not a function. We cannot graph this on our calculator as a single entity, since there is no cardinal for "±". We were non able to solve this equation for a unique (merely one) "y =" equation. Nosotros actually have two "y =" equations: and . (Yes, the graphing reckoner tin can graph these equations separately to form the graph. But the combined graphs volition be a relation, not a office.) The lack of a unique "y =" equation means that y 2 = 10 is non a function. NOTE: The re-posting of materials (in role or whole) from this site to the Internet is copyright violation and is not considered "fair use" for educators. Please read the "Terms of Utilise".

rogerssheire.blogspot.com

Source: https://mathbitsnotebook.com/Algebra1/Functions/FNFuncBasics.html

Share this post